GPU 架构基础 深入理解 GPU 的设计哲学、SIMT 编程模型以及硬件层级映射,建立并行计算的物理直觉。
配套代码
在开始写第一行 CUDA 代码之前,我们需要先调整一下大脑的"计算模式"。
CPU 和 GPU 虽然都是为了计算而生,但它们解决的是完全不同的物理问题。这就好比法拉利 与公交车 的区别:
CPU (Latency Oriented) :为了低延迟 而设计。它拥有巨大的缓存(Cache)和极其复杂的控制逻辑(分支预测、乱序执行)。它的目标是尽快 完成一个必须串行执行的任务。
GPU (Throughput Oriented) :为了高吞吐量 而设计。它砍掉了大部分控制逻辑和缓存,把晶体管全用来造计算单元 (ALU) 。它的目标是同时 处理海量的数据。
GPU 并不是一个能独立运行的计算平台,而必须视为 CPU 的协处理器 (Coprocessor) 。
当我们谈论"GPU 并行计算"时,实际上是指 CPU + GPU 的异构计算架构 :
Host (主机端) :CPU 及其内存。负责复杂的逻辑控制、IO 读取和任务调度。Device (设备端) :GPU 及其显存。负责密集型的并行计算任务。通信桥梁 :两者通过 PCIe 总线 连接。
瓶颈预警 :PCIe 总线的带宽(通常几十 GB/s)远远低于 GPU 内部显存的带宽(通常几 TB/s)。因此,频繁地在 Host 和 Device 之间搬运数据是性能最大的杀手 。编写高效内核的第一原则就是:让数据留在 GPU 上。
登录以继续阅读 这是一篇付费内容,请登录您的账户以访问完整内容。
直观理解 :
如果要把 100 块砖从 A 搬到 B:
CPU 像是一辆法拉利,速度极快,一次搬 2 块,来回跑 50 趟。GPU 像是一群蚂蚁(或者一辆慢速大卡车),速度不快,但一次能搬 100 块,跑 1 趟就搞定。 从硬件图上看,CPU 的芯片大部分面积是 Control 和 Cache ,只有少部分是计算核心。而 GPU 几乎整个芯片都是绿色的计算单元 (ALU)。这种物理结构的差异决定了它们的分工:
特性 CPU GPU 核心数量 较少 (几个到几十个) 众多 (数千个) 擅长任务 控制密集型 (逻辑复杂、分支多)计算密集型 (数据并行、矩阵运算)线程特性 重量级 (上下文切换开销大)轻量级 (极速切换,用于掩盖延迟)
这意味着:GPU 不擅长做复杂的逻辑判断(if-else),但非常擅长做在大规模数据上重复同样的计算。
因此,CPU+GPU 的异构平台正好可以优势互补 :
CPU :负责处理逻辑复杂的串行程序,指挥整个流程。GPU :重点处理数据密集型的并行计算程序,发挥海量核心的算力。 为什么 GPU 会在今天统治 AI 领域?这不仅仅是因为核心多。
随着摩尔定律(Moore's Law)逼近物理极限,单纯靠增加晶体管密度来提升单核性能变得越来越难。图灵奖得主 Hennessy & Patterson 指出,未来的计算性能增长将主要依赖于 特定领域的架构(Domain Specific Architectures) 。
GPU 正是这种理念的先行者:既然无法让一个 工人跑得更快(延迟瓶颈),那就雇佣一万个 工人一起搬砖(吞吐量胜利)。
2007 年,NVIDIA 发布 CUDA ,这是一个里程碑时刻。它允许工程师使用类似 C 语言的代码指挥 GPU,而不再需要伪装成图形渲染任务。这开启了 GPGPU (General-Purpose Computing on GPU) 的时代。
在现代 NVIDIA GPU(Volta 架构之后)中,除了一般的计算核心(CUDA Core),还加入了一种专门为深度学习设计的 Tensor Core 。
CUDA Core :精通通用的标量运算(如 float32 加减乘除)。Tensor Core :只做一件事,但做得快到极致 ——矩阵乘累加(Matrix Multiply-Accumulate, D = A × B + C D = A \times B + C D = A × B + C 这也是为什么在 LLM 推理和训练中,我们总是强调要“用满 Tensor Core”。
为了驾驭这种"人海战术",NVIDIA 提出了 SIMT (Single Instruction, Multiple Threads) 模型。
这是 GPU 编程的核心灵魂:我们不再写循环,而是为每一个数据点分配一个线程。
在 CPU 上做向量加法(Vector Add),我们需要写一个循环:
// CPU: 串行遍历每个元素 void vector_add_cpu ( int * a , int * b , int * c , int n ) { for ( int i = 0 ; i < n; i ++ ) { c [i] = a [i] + b [i]; 而在 GPU 上,这个循环消失了。但在展示 Kernel 之前,让我们先建立一个整体框架:
CUDA 程序的典型执行流程
分配 Host 内存 :在 CPU 侧用 malloc 初始化数据分配 Device 内存 :用 cudaMalloc 在 GPU 侧申请显存拷贝数据到 Device :用 cudaMemcpy 把数据从 CPU 搬到 GPU调用 Kernel ⬅️ 这是本节的重点!拷贝结果回 Host :用 cudaMemcpy 把结果搬回 CPU释放内存 :清理 Host 和 Device 的内存 完整代码见配套仓库 systems/cuda-basics/vector_add_simple.cu
现在,让我们聚焦第 4 步——Kernel 的定义 。我们定义一个 Kernel (核函数),每个线程只负责一个 i:
systems/cuda-basics/vector_add_simple.cu __global__ void cuda_vector_add_simple ( int * OUT, int * A, int * B, int N) { int i = threadIdx.x; // Each thread gets its own ID if (i < N) { OUT[i] = A[i] + B[i];
代码解读 :
__global__:这个关键字告诉编译器,这是一个在 GPU 上执行、从 CPU 调用的函数threadIdx.x:这是 GPU 给每个线程发的"身份证号",替代了 CPU 版本中的循环变量 iif (i < N):边界检查,防止越界访问(下面详细解释) 你可能会问:我需要处理 N 个数据,启动 N 个线程不就刚好吗?为什么还需要 if (i < N)?
答案藏在 GPU 的硬件调度机制里:GPU 的线程是以 Warp(线程束)为单位调度的,每个 Warp 固定包含 32 个线程 。这意味着实际启动的线程数往往不是你想要的精确数字,而是会被"向上取整"到 32 的倍数。
搬砖比喻
想象你在搬家,需要搬 34 块砖头 。你雇佣了工人,但这种工人很奇怪——他们必须以 "8 人小队" 为单位出勤(类似于 32 人的 Warp)。
为了搬完 34 块砖,你不得不请了 5 个小队(共 40 人) 。如果你不告诉他们"只有拿到砖头的人才准搬"(if (i < 34)),那么最后 6 个没拿到砖头的工人就会对着空气乱挥手,甚至可能搬走邻居家的砖头(内存越界 )。
加上这个规定后,那 6 个人就会站在原地发呆(闲置),确保搬运过程不出错。
启动 Kernel 时,我们需要告诉 GPU 启动多少个线程:
// <<<1, N>>> means: 1 Block, N threads cuda_vector_add_simple <<< 1 , N >>> (d_OUT, d_A, d_B, N); 这里的 <<<1, N>>> 是 CUDA 的启动配置语法 ,1 表示只用一个 Block,N 表示启动 N 个线程。由于单个 Block 最多只能有 1024 个线程(现代 GPU 的硬件限制),这个简单版本只能处理小规模数据。下一节我们会学习如何使用多个 Block 来处理百万级数据。
你可能会问:如果我有 100 万个数据,难道要启动 100 万个线程吗?GPU 的硬件能支持吗?
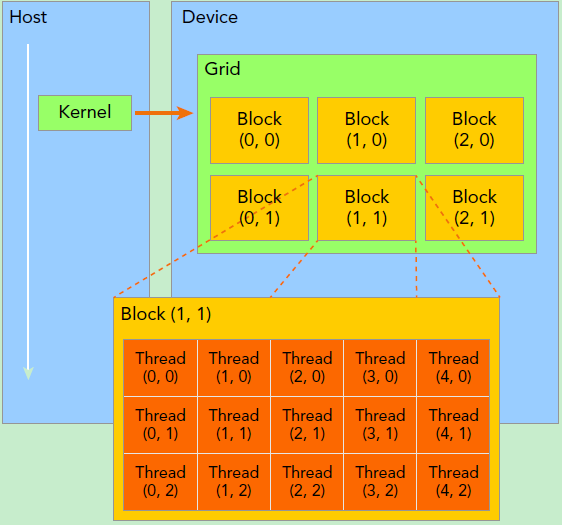
这就引入了 GPU 的层级管理结构。GPU 并不是一个扁平的线程池,而是通过 Grid (网格) -> Block (线程块) -> Thread (线程) 进行组织的。
Grid :一次 Kernel 启动的所有 Block 的集合。Block :线程块,会被调度到某个 SM (Streaming Multiprocessor) 上执行。同一个 Block 内的线程可以通过 Shared Memory 协作。Thread :最小执行单元,32 个 Thread 组成一个 Warp ,这是 GPU 实际调度执行的基本单位。 不同型号的 GPU 有不同的硬件参数。我们可以用 cudaGetDeviceProperties 来查询:
systems/cuda-basics/gpu_info.cu cudaDeviceProp prop; cudaGetDeviceProperties ( & prop, 0 ); // 查询第 0 号 GPU printf ( "SM 数量: %d\n " , prop.multiProcessorCount); printf ( "每 SM 最大 Block: %d\n " , prop.maxBlocksPerMultiProcessor); printf ( "每 Block 最大线程: %d\n " , prop.maxThreadsPerBlock); printf ( "Warp 大小: 参数 值 说明 SM 数量 82 流式多处理器数量 每 SM 最大 Block 数 16 每个 SM 可同时执行的 Block 最大并发 Block 1312 = 82 SM × 16 Block/SM 每 Block 最大线程数 1024 硬件限制 Block 维度上限 (1024, 1024, 64) 每个维度的单独上限 Warp 大小 32 GPU 调度的最小单位
Block 维度 vs 总线程数
Block 可以是多维的(最多 3D),但需要同时满足:
每个维度不超过其上限(如 x ≤ 1024)
总线程数 (x × y × z) 不超过 1024 例如 dim3 block(32, 32, 1) 是有效的(1024 线程),但 dim3 block(32, 32, 2) 无效(2048 线程)。
并发 Block 限制
虽然一个 Grid 可以包含数十亿个 Block,但 GPU 只能同时执行 有限数量(如 1312 个)。超出的 Block 会自动排队,等待空闲 SM 后再调度执行。
一个 Block 最多只能容纳 1024 个线程。要处理百万级数据,我们必须使用多个 Block。
这就需要一个通用的公式,把 Block ID 和 Thread ID 映射成一个唯一的全局索引 :
systems/cuda-basics/vector_add.cu __global__ void cuda_vector_add ( int * OUT, int * A, int * B, int N) { // Global index = Block offset + Thread offset // blockIdx.x: 当前 Block 的编号 (0, 1, 2, ...) // blockDim.x: 每个 Block 有多少个线程 (如 256) // threadIdx.x: 当前线程在 Block 内的编号 (0 ~ blockDim.x-1) int i = blockIdx.x * blockDim.x + threadIdx.x; 在启动 Kernel 时,我们需要计算需要多少个 Block:
const int N = 1000000 ; // 100 万个元素 const int BLOCK_SIZE = 256 ; // 每个 Block 256 个线程 // 向上取整,计算需要多少个 Block int num_blocks = (N + BLOCK_SIZE - 1 ) / BLOCK_SIZE; // = 3907 // 启动 Kernel cuda_vector_add <<< num_blocks, BLOCK_SIZE Launching 3907 blocks with 256 threads each Total threads: 1000192 (for 1000000 elements) Result: ALL 1000000 elements verified OK!
公式拆解
假设 N = 1000000,BLOCK_SIZE = 256:
Block 0: 线程 0-255 处理元素 0-255
Block 1: 线程 0-255 处理元素 256-511
...
Block 3906: 线程 0-255 处理元素 999936-1000191
最后一个 Block 会启动 256 个线程,但只有 64 个线程(i < N)真正工作,其余的会被 if (i < N) 过滤掉。
为什么需要 Block?
SM(流式多处理器)是 GPU 的硬件核心。每个 SM 有自己独立的 Shared Memory 。同一个 Block 内的线程会被调度到同一个 SM 上执行 ,这使得它们可以通过 Shared Memory 进行高速通信。而不同 Block 之间的通信则要困难得多(通常需要走慢速的 Global Memory)。内存层级结构涉及程序优化,这里不深入探讨。
深度学习中处理的大多是矩阵(Matrix)甚至更高维的张量(Tensor)。但在物理层面,GPU 的显存是一维线性 的。
我们需要学会把二维逻辑坐标映射到一维物理地址。这通常涉及到 Row-Major (行主序) 的概念。
在处理矩阵时,我们通常使用二维的 gridDim 和 blockDim。此时,我们需要计算两个维度的全局索引:
行索引 (row) :由 Y 轴的 Block 和 Thread 决定。列索引 (col) :由 X 轴的 Block 和 Thread 决定。 int row = blockIdx.y * blockDim.y + threadIdx.y; int col = blockIdx.x * blockDim.x + threadIdx.x; 有了 (row, col) 后,我们需要将其转换为一维的 Global Memory Index 。在 C/C++ 中,矩阵通常是 行主序 (Row-Major) 存储的,即先存第一行,再存第二行……
// index = 行号 * 总列数 + 列号 int index = row * NUM_COLS + col; systems/cuda-basics/matrix_add.cu __global__ void cuda_matrix_add ( float * OUT, float * A, float * B, int NUM_ROWS, int NUM_COLS) { // 2D global index calculation int row = blockIdx.y * blockDim.y + threadIdx.y; int col = blockIdx.x
交互演示:从 2D 到 1D 的映射
为了直观理解这种映射(Row-Major Layout),请尝试下面的交互演示。移动鼠标查看 2D 坐标如何映射到 1D 物理内存地址。
逻辑视图 (Logical 2D View) Grid: 3x3 blocks · Block: 2x2 threads
Hover over cells to see mapping 物理视图 (Physical 1D Memory)
观察重点:横着读 vs 竖着读
利用上面的交互图,你可以直观地看到为什么访问模式会极大影响 GPU 性能:
行主序(连续访问,快) :
试着横向移动鼠标(Row 0, Col 0 -> 1 -> 2)。下方的物理索引是 0 -> 1 -> 2。这是连续的 。GPU 一次读取(Memory Coalescing)就能把这连续的 32 个数据全抓进来,效率极高。
按列访问(跳跃访问,慢) :
试着纵向移动鼠标(Row 0, Col 0 -> Row 1, Col 0...)。下方的物理索引变成了 0 -> 6 -> 12。这是跳跃的(Strided Access) 。GPU 这时就像一个无奈的快递员,必须跑好多趟才能把散落在不同地址的数据凑齐,导致效率暴跌(Non-Coalesced Memory Access)。
在启动时,我们使用了 dim3 来定义多维的 Grid 和 Block:
// 定义 16x16 的线程块 dim3 block ( 16 , 16 ); // 计算 Grid 维度 (2D) // x 轴对应列 (cols),y 轴对应行 (rows) dim3 grid ( (NUM_COLS + 16 - 1 ) / 16 , (NUM_ROWS + 16 - 1 ) / 16 ); 理解 row_index * NUM_COLS + col_index 这个公式至关重要。
在下一章 Tensor Layout 中,我们将深入探讨这种内存布局对深层学习算子的影响。如果搞反了遍历顺序,性能可能会下降 10 倍以上。
小结
GPU 是吞吐量怪兽 :牺牲单核速度,换取海量并发。SIMT :用 threadIdx 替代 for 循环。层级结构 :Grid -> Block -> Thread 映射了任务 -> SM -> Core 的硬件组织。坐标映射 :一切多维数据最终都要拍扁成一维地址访问。 }
}
}
}
%d\n
"
, prop.warpSize);
if (i < N)
{
OUT[i] = A[i] + B[i];
}
}
>>>
(d_OUT, d_A, d_B, N);
*
blockDim.x
+
threadIdx.x;
if (row < NUM_ROWS && col < NUM_COLS)
{
// Convert 2D (row, col) to 1D index (row-major order)
int index = row * NUM_COLS + col;
OUT[index] = A[index] + B[index];
}
}
cuda_matrix_add <<< grid, block >>> (...);

 CookLLM文档
CookLLM文档